OBJETIVO VISIÓN Y MISIÓN

Con este blog pretendemos que los/as alumnos/as descubran la belleza de la matemáticas, que la sepan apreciarla en las formas de la naturaleza, en el arte, en su día a día etc. Es importante que entiendan su necesidad en la vida cotidiana .Como dice Galileo “Las matemáticas son el lenguaje de la Naturaleza.”

CASOS PARTICULARES DE LA HIPERBOLA

Hipérbola equilátera

Una hipérbola equilátera es aquella en la cual el semieje real es de igual longitud que el semieje imaginario. Es decir que su ecuación puede ser de la forma:

$$\frac{x^2}{a^2}–\frac{y^2}{a^2}=1obien–\frac{x^2}{a^2}+\frac{y^2}{a^2}=1$$

Hipérbolas conjugadas

Dos hipérbolas son conjugadas una de la otra si el eje real de cada una de ellas es igual al eje imaginario de la otra.

En términos analíticos se las reconoce porque los signos están cambiados, y los coeficientes de $x$ y de $y$ siguen siendo los mismos en términos absolutos. Las siguientes hipérbolas son conjugadas:

$$H_1:\frac{x^2}{p^2}–\frac{y^2}{q^2}=1H_2–\frac{x^2}{p^2}+\frac{y^2}{q^2}=1$$

Gráficamente:

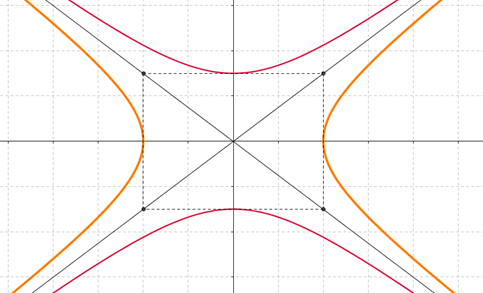
Cómo se aprecia en la gráfica las hipérbolas conjugadas tienen iguales asíntotas.

Recopilado de (https://aga.frba.utn.edu.ar/hiperbola/ )

Elementos de la hipérbola

Los elementos de la hipérbola son:

• Focos: son los dos puntos fijos (F₁ y F₂).
• Radio vector: es la distancia R de un punto de la hipérbola (P) a cualquiera de los focos.
• Eje focal: es el eje de simetría E que une a los dos focos. También se llama eje transverso.
• Eje no transverso: es la mediatriz T del eje focal.
• Centro: es el punto medio O de los dos focos. También se puede definir como la intersección del eje focal y el transverso.
• Vértices: son los dos puntos de intersección del eje focal con la hipérbola (V₁y V₂).

• Distancia focal: es la distancia 2centre focos. También se denota como F₁F₂.
• Eje real: es es la distancia 2a entre vértices.
• 
  
• Eje imaginario: es la distancia 2b de los puntos B₁ y B₂. Los puntos B₁ y B₂ se generan como vemos en las relaciones entre semiejes.
  Así pues, existe una relación entre los semiejes y la distancia focal:
  
• Asíntotas: son las líneas rectas (A₁ y A₂) que se aproximan a la hipérbola en el infinito.
• Puntos interiores y exteriores: la hipérbola divide el plano en tres regiones. Dos regiones que contienen un foco cada una y otra región sin ningún foco. Los puntos contenidos en las regiones con un foco se llaman interiores (I) y los otros exteriores (Ex).
• Tangentes de la hipérbola: sobre cada punto P_i de ambas ramas de la misma. Cada tangente es la bisectriz de los dos radios vectores del punto P

Recopilado de (https://www.universoformulas.com/matematicas/geometria/hiperbola/ )

EJEMPLOS ECUACIONES CANONICA Y ORDINARIA

EJERCICIOS DE HIPERBOLA

DESCARGAR

EJEMPLO DE ECUACIONES DE LA HIPÉRBOLA

ECUACIONES DE LA HIPERBOLA

Ecuación reducida de la hipérbola

F'(-c,0) y F(c,0)

Ecuación de la hipérbola con los focos en el eje OY

F'(0, -c) y F(0, c)

Ecuación de la hipérbola con eje paralelo a OX, sin centro el origen

Donde A y B tienen signos opuestos.

Ecuación de la hipérbola con eje paralelo a OY, sin centro el origen

Ecuación de la hipérbola equilátera

Asíntotas

, 

Excentricidad

Ecuación de la hipérbola equilátera respecto a sus asíntotas

Recopilado de (https://www.vitutor.net/1/34.html )